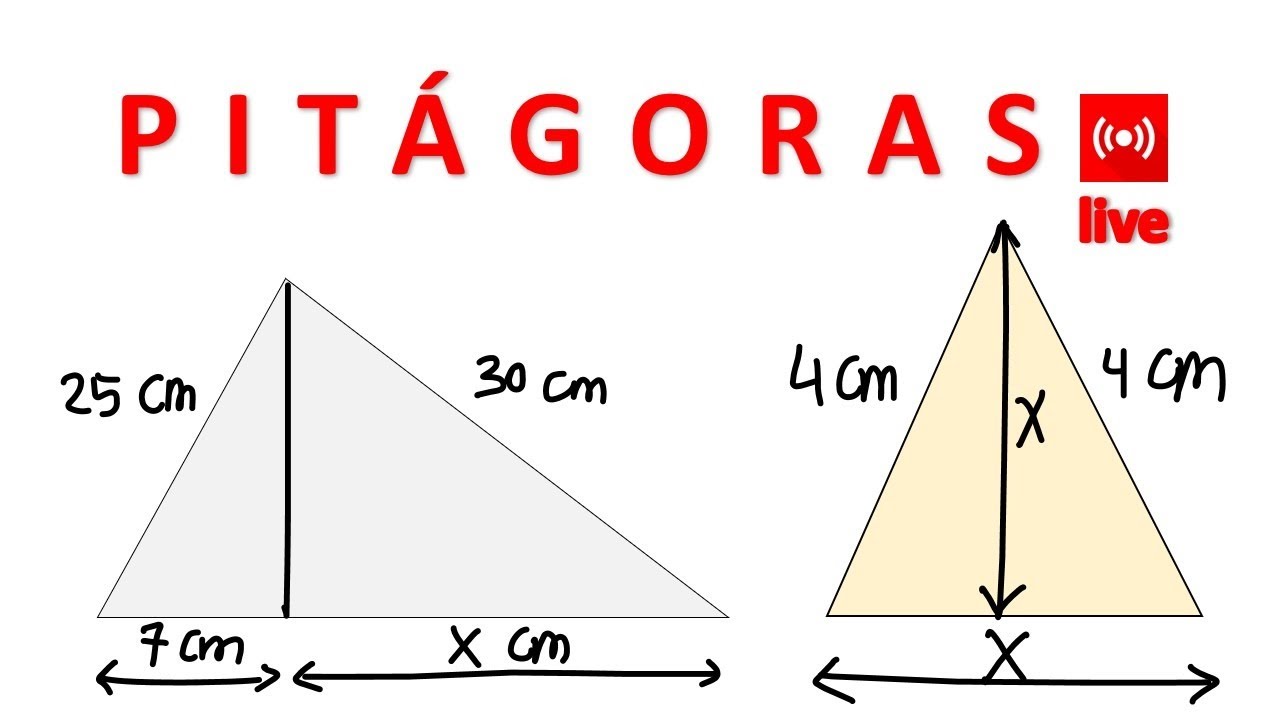
Learn Pythagorean Theorem: Solved Exercises

ivana 13 Jun 2024

If you're looking to master the Pythagorean theorem, look no further! Our comprehensive guide, complete with solved exercises, is your ultimate resource.

The Pythagorean theorem is a fundamental concept in geometry that relates the lengths of the sides of a right triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In other words, if a, b, and c represent the lengths of the sides of a right triangle, then a + b = c.

This theorem has countless applications in various fields, including architecture, engineering, and physics. It allows us to calculate unknown side lengths of right triangles and solve problems involving distances and angles. Throughout history, the Pythagorean theorem has played a pivotal role in shaping our understanding of geometry and trigonometry.

The Pythagorean Theorem

The Pythagorean theorem is a cornerstone of geometry, with applications in architecture, engineering, and physics. Its essence lies in the relationship between the lengths of the sides of a right triangle.

Definition: The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides.
Formula: a + b = c, where a and b are the lengths of the legs of the triangle and c is the length of the hypotenuse.
Applications: Calculating unknown side lengths, determining distances, and solving angle-related problems.
Historical Significance: Attributed to the Greek mathematician Pythagoras, the theorem has been known and used for centuries.
Educational Value: A fundamental concept in geometry, it fosters problem-solving skills and spatial reasoning.

The Pythagorean theorem continues to be a vital tool in various fields, providing a solid foundation for understanding geometry and trigonometry. It exemplifies the power of mathematics in describing the relationships between shapes and quantities.

Definition

This definition encapsulates the essence of the Pythagorean theorem, providing a mathematical formula that precisely describes the relationship between the sides of a right triangle. It serves as the foundation for understanding and applying the theorem in various contexts.

Calculating Unknown Side Lengths: The Pythagorean theorem allows us to determine the length of an unknown side of a right triangle if the lengths of the other two sides are known. This is particularly useful in fields such as architecture and engineering, where precise measurements are crucial.
Determining Distances: The theorem finds applications in determining distances between points, especially in situations where direct measurement is impractical. For instance, surveyors use the Pythagorean theorem to calculate distances across inaccessible terrains.
Solving Angle-Related Problems: The Pythagorean theorem is closely intertwined with trigonometry, the study of angles. It provides a fundamental connection between the sides and angles of a right triangle, enabling us to solve problems involving angle measures.
Educational Significance: The Pythagorean theorem is a cornerstone of geometry education, fostering problem-solving skills and spatial reasoning abilities. It introduces students to the concept of mathematical proofs and the power of deductive reasoning.

In essence, the Pythagorean theorem is a fundamental tool that transcends theoretical mathematics, finding practical applications in diverse fields. Its ability to relate the sides of a right triangle has made it an indispensable concept in geometry, trigonometry, and beyond.

Formula

The formula a + b = c is the mathematical representation of the Pythagorean theorem. It establishes a precise relationship between the lengths of the sides of a right triangle, providing a fundamental tool for solving problems involving right triangles.

Within the context of "teorema de pitagoras ejercicios resueltos teorema de," this formula serves as the cornerstone for understanding and applying the Pythagorean theorem in practical scenarios. It allows us to calculate unknown side lengths, determine distances, and solve angle-related problems.

For instance, in architecture, engineers use the Pythagorean theorem to calculate the lengths of rafters and other structural components in buildings. In surveying, it is employed to determine distances across inaccessible terrains. The formula also finds applications in physics, where it is used to calculate the magnitude of vectors and solve problems involving projectile motion.

The formula a + b = c is not just a mathematical equation but a powerful tool that underpins the practical applications of the Pythagorean theorem. It empowers us to solve real-world problems, making it an indispensable concept in various fields.

Applications

The Pythagorean theorem finds practical applications in various fields, including architecture, engineering, and surveying. It provides a powerful tool for solving problems involving right triangles, enabling us to calculate unknown side lengths, determine distances, and solve angle-related problems.

For instance, in architecture, engineers rely on the Pythagorean theorem to calculate the lengths of rafters and other structural components in buildings. By knowing the lengths of two sides of a right triangle, they can use the theorem to determine the length of the third side, ensuring the structural integrity of the building.

Similarly, in surveying, the Pythagorean theorem is employed to determine distances across inaccessible terrains or bodies of water. Surveyors use the theorem to calculate the distance between two points by forming a right triangle and measuring the lengths of the legs. This technique is particularly useful in situations where direct measurement is impractical or impossible.

The Pythagorean theorem also plays a crucial role in solving angle-related problems. In trigonometry, the sine, cosine, and tangent functions are defined using the ratios of the sides of a right triangle. By understanding the relationship between the sides and angles of a right triangle, we can use the Pythagorean theorem to solve problems involving angles, such as determining the angle of elevation or depression.

In essence, the Pythagorean theorem is not merely a mathematical concept but a practical tool that underpins various applications across different fields. Its ability to relate the sides and angles of a right triangle empowers us to solve real-world problems, making it an indispensable concept in architecture, engineering, surveying, and beyond.

Historical Significance

The historical significance of the Pythagorean theorem lies at the very core of understanding "teorema de pitagoras ejercicios resueltos teorema de." As a fundamental concept in geometry, the Pythagorean theorem has been known and used for centuries, shaping the development of mathematics and its applications.

Pythagoras, a Greek mathematician who lived in the 6th century BC, is widely credited with the discovery of the Pythagorean theorem. However, historical evidence suggests that the theorem was known and used by Babylonian mathematicians even earlier. Regardless of its origins, the theorem has had a profound impact on the advancement of mathematics and its practical applications.

The enduring significance of the Pythagorean theorem stems from its fundamental nature. It provides a simple yet powerful relationship between the sides of a right triangle, enabling us to solve a wide range of problems involving right triangles. This has made the Pythagorean theorem an indispensable tool in various fields such as architecture, engineering, surveying, and navigation.

In architecture, the Pythagorean theorem is used to calculate the lengths of rafters and other structural components, ensuring the stability of buildings. In engineering, it is employed to determine the forces acting on structures and to design efficient and safe structures. In surveying, the Pythagorean theorem is used to calculate distances and determine the areas of land. In navigation, it is used to calculate the distance between two points on a map or chart.

The historical significance of the Pythagorean theorem is inextricably linked to "teorema de pitagoras ejercicios resueltos teorema de." By understanding the historical context and development of the theorem, we gain a deeper appreciation for its importance and the role it has played in shaping our understanding of geometry and its applications.

Educational Value

The educational value of the Pythagorean theorem, as a fundamental concept in geometry, is deeply intertwined with "teorema de pitagoras ejercicios resueltos teorema de." The theorem provides a solid foundation for developing problem-solving skills and spatial reasoning abilities, which are essential for success in STEM fields and beyond.

By engaging with exercises and solved problems related to the Pythagorean theorem, students learn to apply the theorem to solve a variety of problems involving right triangles. They develop their ability to visualize and manipulate geometric shapes, identify patterns, and make logical deductions. These skills are crucial for critical thinking and problem-solving in real-world scenarios.

For instance, architects and engineers rely on the Pythagorean theorem to design and construct buildings and structures. They need to be able to calculate the lengths of rafters, determine the angles of roofs, and ensure the stability of their designs. The theorem also finds applications in navigation, surveying, and other fields where spatial reasoning and problem-solving skills are essential.

In summary, the educational value of the Pythagorean theorem, as a fundamental concept in geometry, is central to "teorema de pitagoras ejercicios resueltos teorema de." By understanding the theorem and practicing its applications, students develop valuable problem-solving skills and spatial reasoning abilities, which are indispensable for success in various fields.

Frequently Asked Questions about "Teorema de Pitgoras

This section addresses common questions and misconceptions surrounding the Pythagorean theorem and its applications.

Question 1: What is the Pythagorean theorem?

The Pythagorean theorem is a fundamental theorem in geometry that relates the lengths of the sides of a right triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Question 2: How can I use the Pythagorean theorem to solve problems?

To use the Pythagorean theorem to solve problems, you need to know the lengths of two sides of a right triangle. You can then use the theorem to find the length of the third side.

Question 3: What are some real-world applications of the Pythagorean theorem?

The Pythagorean theorem has many real-world applications, including architecture, engineering, and surveying. For example, architects use the theorem to calculate the lengths of rafters, while engineers use it to determine the forces acting on structures.

Question 4: What is the historical significance of the Pythagorean theorem?

The Pythagorean theorem has a rich historical significance. It is attributed to the Greek mathematician Pythagoras, who lived in the 6th century BC. However, there is evidence that the theorem was known and used by Babylonian mathematicians even earlier.

Question 5: What are some common misconceptions about the Pythagorean theorem?

One common misconception about the Pythagorean theorem is that it only applies to right triangles. However, the theorem actually applies to all triangles, regardless of their shape.

Question 6: How can I improve my understanding of the Pythagorean theorem?

There are several ways to improve your understanding of the Pythagorean theorem. One way is to practice solving problems involving the theorem. You can also read about the history of the theorem and its applications in different fields.

In summary, the Pythagorean theorem is a fundamental theorem in geometry with a wide range of applications in the real world. By understanding the theorem and its applications, you can develop valuable problem-solving skills and spatial reasoning abilities.

Conclusion

The Pythagorean theorem is a cornerstone of geometry, providing a fundamental relationship between the sides of a right triangle. Its applications extend far beyond the classroom, making it an indispensable tool in fields such as architecture, engineering, and surveying. Understanding the Pythagorean theorem and practicing its applications fosters problem-solving skills and spatial reasoning abilities.

The theorem's enduring significance lies in its simplicity and versatility. It empowers us to solve a wide range of problems involving right triangles, from calculating unknown side lengths to determining distances and angles. By engaging with exercises and solved problems, we deepen our understanding of the theorem and its practical applications.

The Ultimate Guide To Www.sehuatang.org: Your Key To Understanding
The Unstoppable Freecell.fr: Play Freecell For Free!
Evocative Tales Of Punished Schoolgirls: Exploring Consequences And Redemption