How many nets are there for a square based pyramid?
A square-based pyramid has five nets. A net is a two-dimensional representation that can be folded into a three-dimensional model. The five nets for a square-based pyramid are:
- Square base
- Four triangles that form the sides of the pyramid
The square base is the only regular polygon that can be used to form a square-based pyramid. The four triangles that form the sides of the pyramid can be equilateral, isosceles, or scalene.
Nets are important because they can be used to create three-dimensional models of objects. This can be helpful for understanding the geometry of an object or for creating a physical model for a project.
The nets for a square-based pyramid are relatively simple to create. This makes them a good project for students who are learning about geometry or for anyone who wants to create a simple three-dimensional model.
How many nets for square based pyramid
A square-based pyramid has five nets, which are two-dimensional representations that can be folded into three-dimensional models. The five nets for a square-based pyramid are:
- Square base
- Four triangles that form the sides of the pyramid
The square base is the only regular polygon that can be used to form a square-based pyramid. The four triangles that form the sides of the pyramid can be equilateral, isosceles, or scalene.
Nets are important because they can be used to create three-dimensional models of objects. This can be helpful for understanding the geometry of an object or for creating a physical model for a project.
The nets for a square-based pyramid are relatively simple to create. This makes them a good project for students who are learning about geometry or for anyone who wants to create a simple three-dimensional model.
Square base
A square base is a polygon with four equal sides and four right angles. It is the only regular polygon that can be used to form a square-based pyramid.
- Number of sides: A square base has four sides.
- Length of sides: All four sides of a square base are equal in length.
- Angles: A square base has four right angles.
- Area: The area of a square base is calculated by multiplying the length of one side by itself.
The square base is an important part of a square-based pyramid. It provides the foundation for the pyramid and determines the shape of the pyramid's sides. Without a square base, a square-based pyramid would not be able to stand up.
Four triangles that form the sides of the pyramid
A square-based pyramid has four triangles that form the sides of the pyramid. These triangles are congruent, meaning that they have the same size and shape. The triangles are isosceles triangles, meaning that they have two equal sides and one unequal side. The unequal side is the base of the triangle, and the equal sides are the legs of the triangle.
The four triangles that form the sides of the pyramid are important because they determine the shape of the pyramid. Without these triangles, the pyramid would not be able to stand up. The triangles also provide support for the pyramid, preventing it from collapsing.
The number of nets for a square-based pyramid is directly related to the number of triangles that form the sides of the pyramid. A square-based pyramid has five nets, and each net includes four triangles. This is because each net is a two-dimensional representation of the three-dimensional pyramid, and each triangle in the net represents one of the four triangles that form the sides of the pyramid.
Understanding the connection between the four triangles that form the sides of the pyramid and the number of nets for a square-based pyramid is important for understanding the geometry of pyramids. This understanding can be used to create three-dimensional models of pyramids, to calculate the surface area and volume of pyramids, and to solve problems involving pyramids.
FAQs on Square-Based Pyramids
This section addresses frequently asked questions about square-based pyramids to enhance understanding of their geometry and properties.
Question 1: How many nets does a square-based pyramid have?
Answer: A square-based pyramid has 5 nets, which are two-dimensional representations that can be folded into a three-dimensional pyramid.
Question 2: What is the shape of the base of a square-based pyramid?
Answer: The base of a square-based pyramid is a square, which is a regular polygon with four equal sides and four right angles.
Question 3: How many sides does a square-based pyramid have in total?
Answer: A square-based pyramid has 5 sides in total: the square base and four triangular sides.
Question 4: Are the sides of a square-based pyramid always congruent?
Answer: Yes, the sides of a square-based pyramid are always congruent isosceles triangles, meaning they have two equal sides and one unequal side.
Question 5: What is the relationship between the number of nets and the shape of the base of a pyramid?
Answer: The number of nets for a pyramid is directly related to the shape of its base. For example, a square-based pyramid has 5 nets, while a triangular-based pyramid has 4 nets.
Question 6: What is the importance of understanding the geometry of square-based pyramids?
Answer: Understanding the geometry of square-based pyramids is important for various applications, such as architecture, engineering, and design. It enables calculations of surface area, volume, and stability, which are crucial for constructing and analyzing structures involving pyramids.
Summary: Square-based pyramids have 5 nets, a square base, and 4 congruent isosceles triangular sides. Understanding their geometry is essential for practical applications, including architecture and engineering.
Next Section: Applications of Square-Based Pyramids
Conclusion
In summary, the exploration of "how many nets for square based pyramid" has revealed that a square-based pyramid possesses five distinct nets. These nets serve as two-dimensional representations that can be folded into three-dimensional models of the pyramid. The unique shape of the square base and the four congruent triangular sides contribute to the pyramid's structural stability and geometric properties.
Understanding the geometry of square-based pyramids extends beyond mere academic knowledge. It finds practical applications in fields such as architecture, engineering, and design. Architects and engineers utilize this knowledge to design and construct stable structures, while designers employ it to create visually appealing objects. Furthermore, understanding the relationship between the number of nets and the shape of the base is essential for analyzing and solving problems involving pyramids.
Uncover The Significance Of The Stars On Cards Against Humanity: A Comprehensive Explanation
Discover The Thrilling World Of Komogvind DK Games
Best MKVMoviesPoint: Free & Fast HD Movies Download
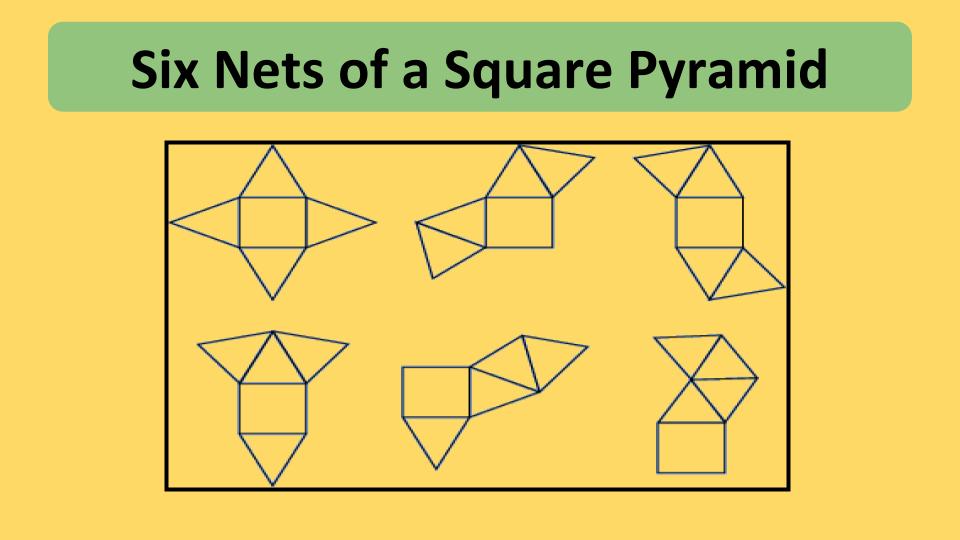
Ms Rashid Geometry Possible Nets for a Square Pyramid

Math, Grade 7, Zooming In On Figures, Gallery Problems Exercise OER
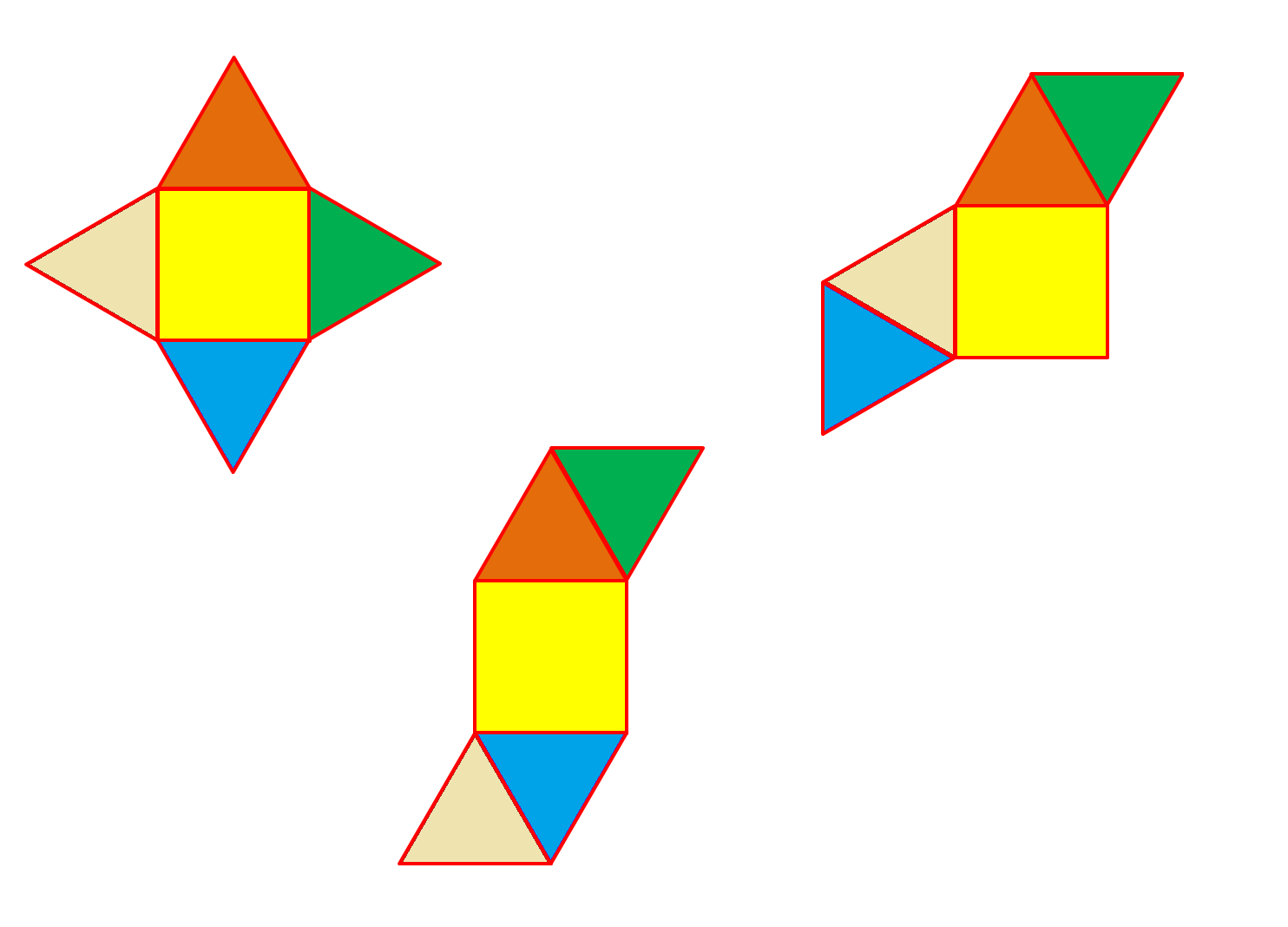
MEDIAN Don Steward mathematics teaching other numbers of nets